
折纸盒问题一直是行测图形推理中一个非常重要的考点。很多考生遇到折纸盒问题的时候,感觉做题慢,就会抱怨、放弃,特别是四面体可能根本想不到怎么去折叠。今天我们就一起来帮大家解决四面体的折纸盒问题。不需要你的空间想象能力,只要平面的知识降这一问题会迎刃而解,下面就跟大家一起来看四面体的折纸盒:
一、什么是四面体
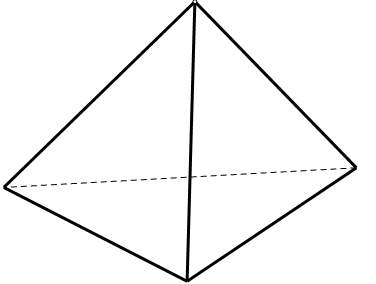
1.四面体的立体图和展开图:由四面组成,每三个面都含有公共顶点。
2.四面体的展开图中如何判断四面体相邻面:
(1)展开图中构成一条直线的两条边是同一条边
(2)平行四边形两个短边是同一条边
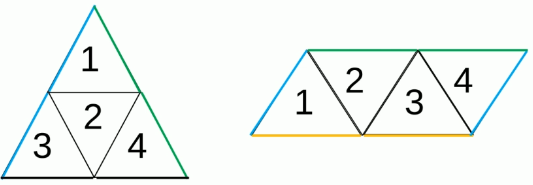
图1 图2
展开图中构成一条直线的两条边是同一条边:图1中标蓝色、绿色、黑色的两条边均是同一条边;图2中标绿色、黄色的两条边是同一条边。
平行四边形两个短边是同一条边:图2的外框是平行四边形,两端蓝色的短边是同一条边。
二、解题思维:排除错误选项,即用平面的思维去做题,排除掉错误的选项,剩下的就是正确答案。
三、四面体解题方法:公共边法
公共边法:两个相邻面的公共边与两个面的相对位置不变
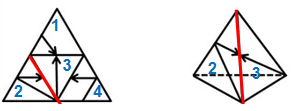
图1 图2
图2中的两个面分别是图1中的面2和面3,面2和面3的公共边在展开图中与面3的箭头并不垂直,但是在立体图中,面3的箭头垂直于面2和面3的公共边,所以展开图与平面图不一致,可以排除。
题型示例
左边给定的是纸盒外表面的展开图,右边哪一项能够由它折叠而成:

四个选项中都是面2和面4,所以可以画出面2和面4的公共边,面2的虚线与公共边相交却不垂直,可以排除C、D两个选项,面4的两个短线与公共边都相交,排除B项,所以选择A项。

在梳理清楚,掌握好方法之后,四面体折叠分并不难。我们需要识别好四面体中哪些边是公共边,才能更好的运用公共边法。因此大家在做题的时候有针对性的安排复习,并预祝广大考生在考试中取得优异成绩!