
前 言
特殊增长率包括间隔增长率、年均增长率、混合增长率类三种题型。
间隔增长率
题型识别:
时间间隔一年,求增长率。
例:求2018年相比2016年的增长率是多少。
公式:r=r1+r2+r1×r2
首先要我们明确r1和r2怎么找,如果说求2018年相比2016年的增长率,那么r1 是2018年的同比增长率,r2是2017年的同比增长率。
其次是计算,主要分为两种情况:其一如果说r1与r2的绝对值均小于10%时,r1×r2可以忽略。例:5%+8%+5%×8%=?5%和8%的绝对值均小于10%,此时5%×8%=0.4%,相对于5%+8%近似可以忽略不计,所以5%+8%+5%×8%≈13%;其二如果说不可以忽略,计算时其中一个不变,另外一个进行百化分即可。例:18%+33.3%+18%×33.3%=?18%和33.3%的绝对值均大于10%,不可以忽略,此时可以把其中一个进行百化分,33.3%约等于1/3,则18%+33.3%+18%×33.3%≈51.3%+18%×1/3=57.6%。
最后在考试中间隔增长也会延伸成间隔基期等题型:
间隔基期公式:基期量(间)=现期量/(1+r间)
间隔倍数公式:倍数(间)=r间+1。
关键都是在于求出r间,进而求出其他量即可。
例题演示
【材料】
2023年1-7月份,全国规模以上工业企业实现利润总额39439.8亿元,同比下降15.5%,增速比上年同期回落16.6个百分点。
【题干】
2023年1-7月份,全国规模以上工业企业实现利润总额约比2021年1-7月份( )。
A.下降了13.8%
B.增长了13.8%
C.下降了31.5%
D.增长了31.5%
【答案】A
【解析】

年均增长率
题型识别:
年均增长最快是哪个、年均增速排序以及求年均增速等。
例:2016年与2012年相比,年均增长率最高的是哪一指标。
公式:

在考试中常考的是比较类,方法也很简单,n相同,比较现期量/基期量即可。年均增长类问题确定现期和基期尤为重要,例如2011年-2015年基期为2011年,现期为2015年,年份差n=4。如果说是五年规划,例如十二五(2011年-2015年),此时基期需往前推一年,则基期为2010年,现期为2015年,年份差n为5。
例题演示
【材料】
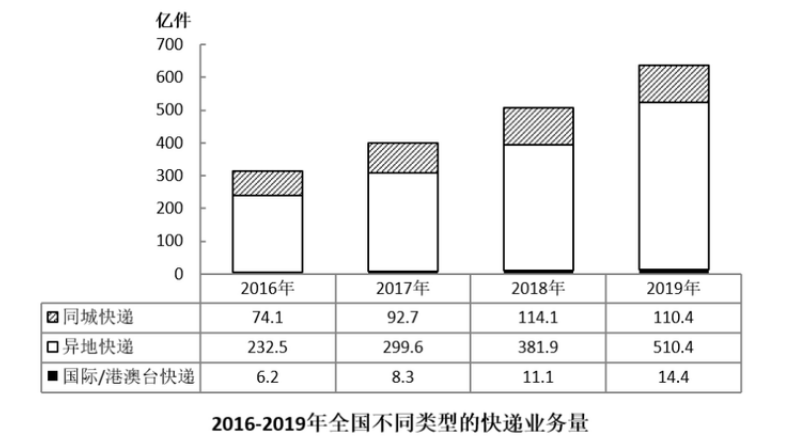
【题干】
将①同城快递、②异地快递、③国际/港澳台快递按2016-2019年业务量年均增速(以2016年为基期)从高到低排列,以下正确的是:
A.①②③
B.①③②
C.③①②
D.③②①
【答案】D
【解析】

混合增长率
题型识别:
明显有部分混合得到总体的关系,求增长率。
例:已知:2021 年 1—4 月份,第二产业投资 42255 亿元,同比增长 21.7%;第三产业投资 97929 亿元,同比增长 18.7%。
问题:2021 年 1—4 月第二、第三产业投资之和比去年同期增长( )。
A. 18.7%
B. 20.2%
C. 20.5%
D. 19.6%
解题方法:
口诀:混合后居中不正中,偏向基期量较大的部分;精算:距离与量成反比。
例题演示
【材料】
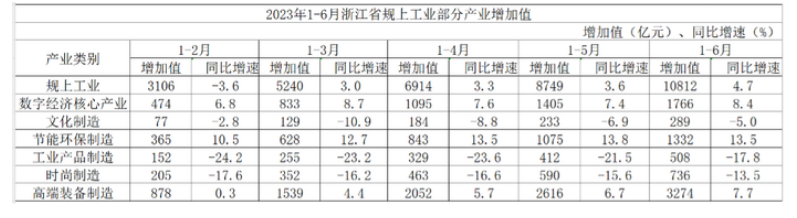
【题干】
2023年二季度,浙江省规上工业增加值同比增速约为多少?( )
A.2%
B.4%
C.6%
D.8%
【答案】C
【解析】
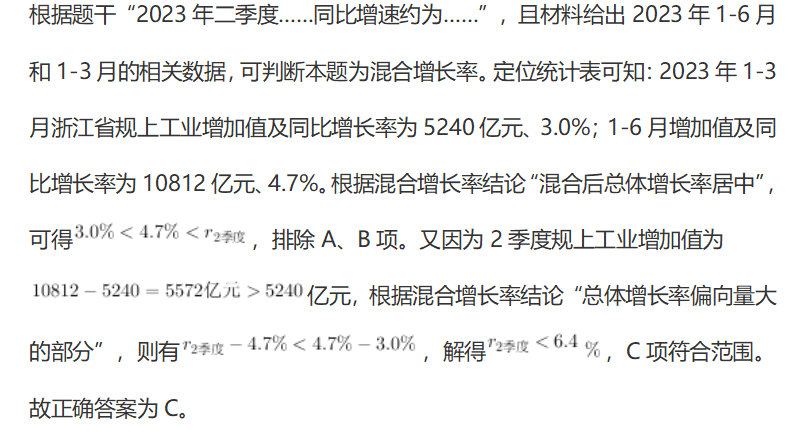
小粉笔总结
综上,特殊增长率题型相对来讲难一些,但是我们记住了各自的套路、方法,还是容易去做出来的,关键在于刷题时巩固方法,方法熟练了,做题速度就会明显提高。最后,小粉笔祝大家都能考出一个好成绩!