“立体拼合”实用技巧
例题演练
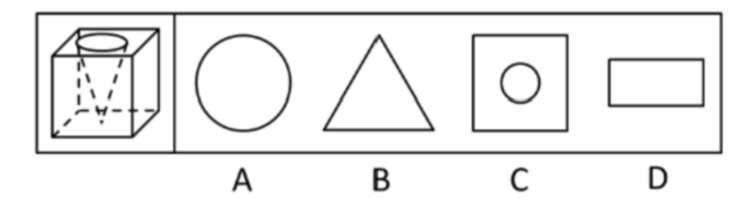
【例1】(2021四川)要想使右侧图形在不旋转的情况下拼合成左侧的正方体造型,还需在问号处添加的图形是:
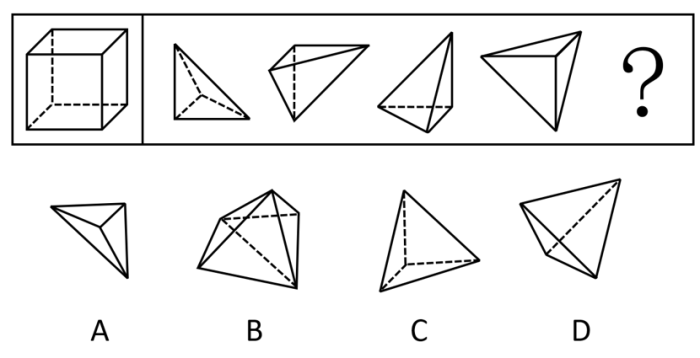
【题型判定】通过问题可直接判断题型为立体拼合,即选项图形可以和右边图形拼合成正方体。
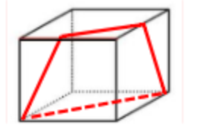
【题目分析】本题考查立体拼合。观察发现,右侧四个图形包含左侧正方体的所有外表面(可通过12个直角三角形面进行判断),因此“?”处图形无法与直角三角形面进行拼合,需与右侧四个图形中非直角三角形面(4个)进行拼合,只有D项符合。具体拼合如下图所示:
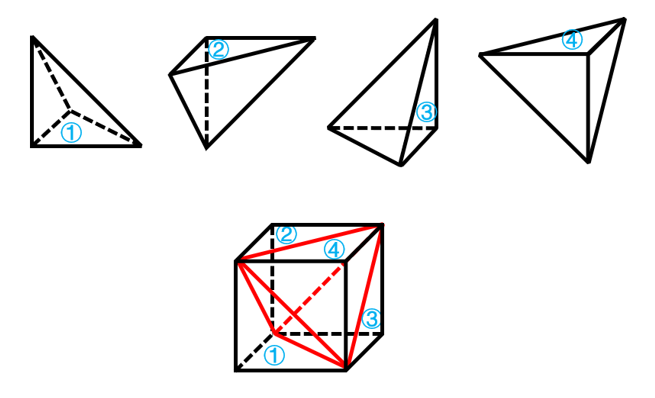
故正确答案为D。
粉笔小贴士
1.立体拼合题目无需观察整体是否可以拼合,只需观察图形特殊的“凹凸”的部分,同时要多利用排除法做题。
2.立体拼合的题目需要明确所需拼合的图形是否能够旋转或翻转,注意题干所提供的信息。
【例2】(2020国考)左图给定的是由相同正方体堆叠而成多面体的正视图和后视图。该多面体可以由①、②和③三个多面体组合而成,问以下哪一项能填入问号处?
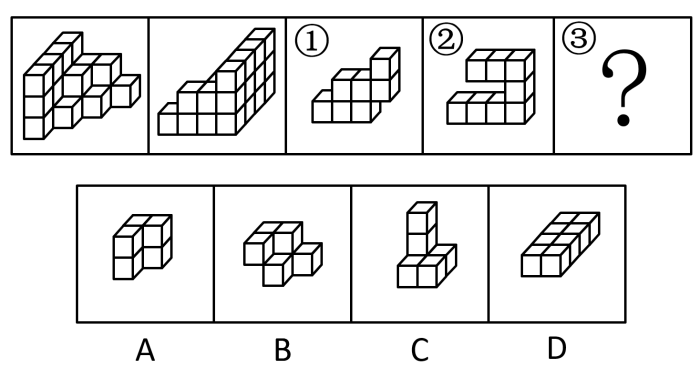
【题型判定】通过问题可判定本题考查立体拼合,即选项与图形①②共同拼合成左边的立体图形。
【题目分析】本题考查立体拼合。
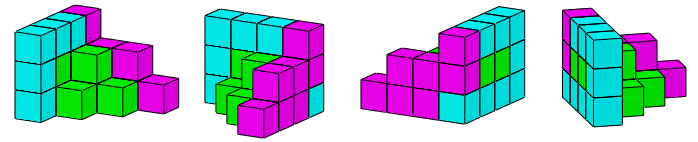
观察题干给出的多面体可知,横行和竖列最多均有4个正方体,其中②最下方为4个正方体,①最下方可以拼为4个正方体,则①和②正方体数量最多的行列会放置在主视图的左后方。根据题干后视图可知,第二层最多有3个小立方体,①第二行有3个小立方体,所以①在后视图的最前面,并且②最下面多出来的正方体可以和①最下方缺少的正方体进行拼合,如上图所示。拼合后可知,第二层缺少3个正方体,排除C、D两项。对比A、B两项可知,下层的正方体位置不同,①②拼合后最左侧不缺正方体,据此B项当选。
故正确答案为B。
粉笔小贴士
1.小方块立体拼合的题目近年来频繁出现,是命题的趋势,如果选项小方块数量不同,可先根据小方块的数量进行排除。
2.优先找块数最多或者形状特殊(和立体图形的某一部分相同)的开始拼,能确定一些位置后,可以再“分层”去找一些缺块。
3.当选项图形与题干残缺图形无法满足“凹凸一致”的原则时,可尝试将题干图形或选项图形进行简单的旋转与翻转,再利用“凹凸一致”原则进行验证。
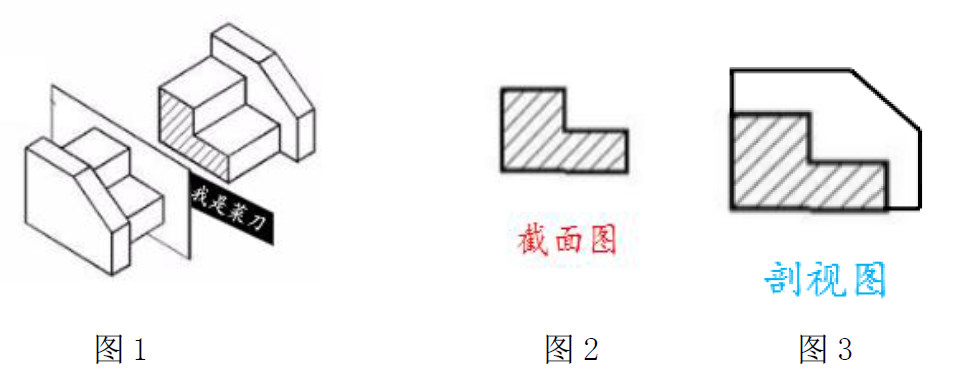
“截面图”必会技巧
例题演练
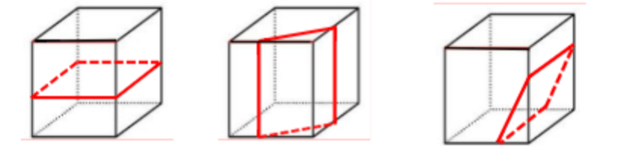
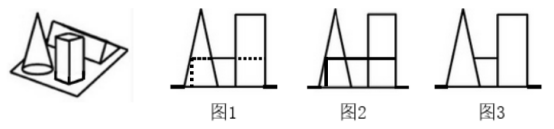
【例1】(2023浙江)左图为给定的多面体,将其从任一面剖开,哪项不可能是该多面体的截面?
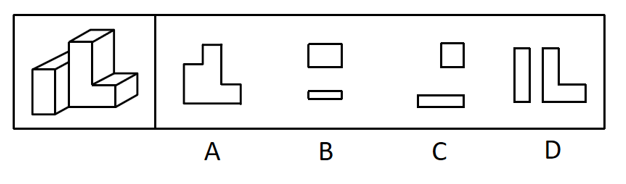
【题型判定】通过问题可以判断本题考查截面图,要求选出的是不可能成为截面的选项。
【题目分析】本题考查截面图,逐一分析选项。
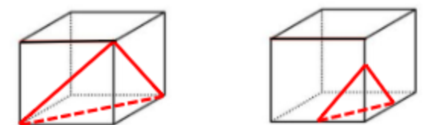
A项:如下图所示,可以截出,排除;
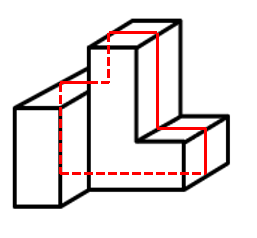
B项:如下图所示,可以截出,排除;
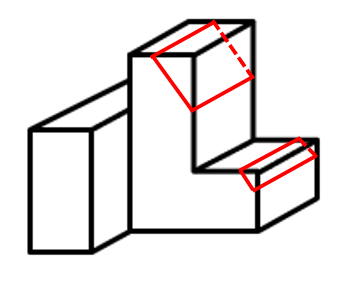
C项:如下图所示,可以截出,排除;
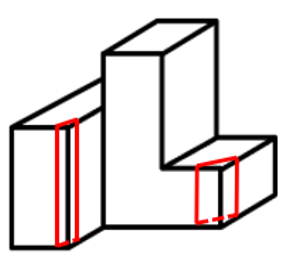
D项:无法截出,当选。
本题为选非题,故正确答案为D。
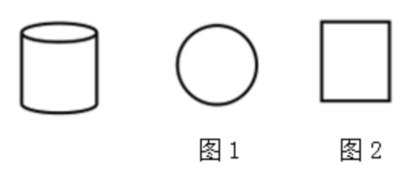
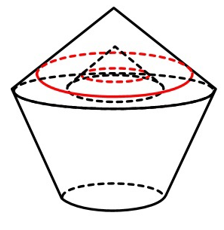
【例2】(2022国考)左图是给定的空心立体图形,将其从任一面剖开,以下哪项可能是该立体图形的截面?
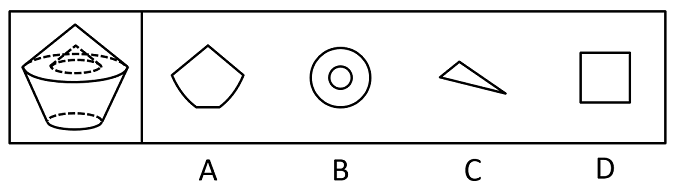
【题型判定】通过问题可以判断本题考查截面图,要求选出的是可能成为截面的选项。
【题目分析】本题考查截面图,逐一分析选项。
A项:无法切出,排除;
B项:从图形上半部分横着切,经过中间空心部分即可得到,当选;
C项:无法切出,排除;
D项:无法切出,排除。
故正确答案为B。
粉笔小贴士
1.截面题题目问题多要求选择“不可能”的截面选项;
2.当整体无法判断图形的截面图时,可分解成基础图形进行判断;
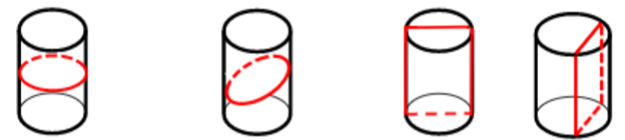
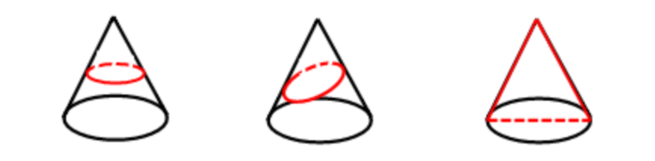
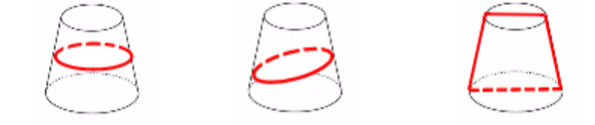
3.熟练掌握常见的六面体、圆柱、圆锥、圆台等基础图形的各种截面形状。
“三视图”做题思路
例题演练
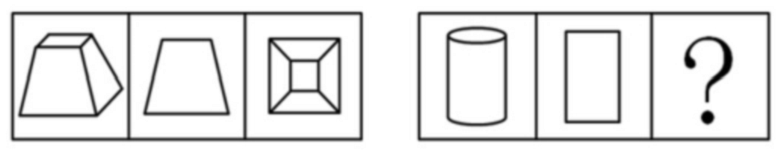
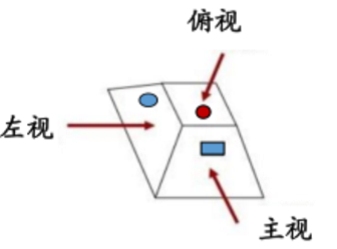
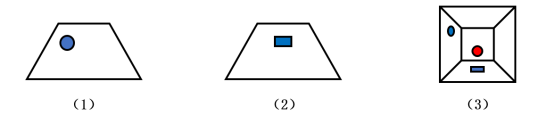
【例1】(2023安徽)下方为某一立体图形的侧视图、正视图和顶视图,请从下列选项中选出与之符合的一项:
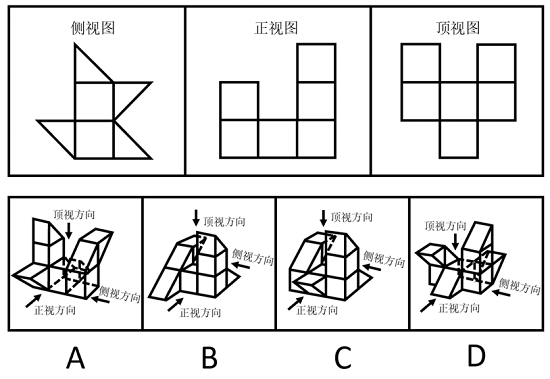
【题型判定】通过题目问题可直接判定本题考查三视图。
【题目分析】本题考查三视图,逐一分析选项。
A项:选项的正视图、顶视图如下图所示,与题干不符,排除;
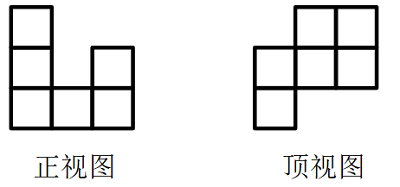
B项:选项的侧视图、顶视图如下图所示,与题干不符,排除;
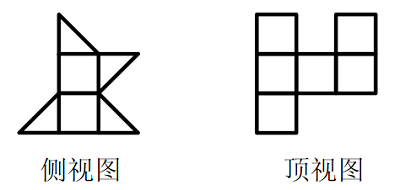
C项:选项的侧视图、正视图和顶视图,均与题干相符,当选;
D项:选项的侧视图、顶视图如下图所示,与题干不符,排除。
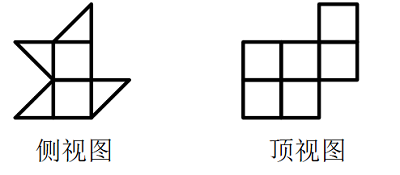
故正确答案为C。
【例2】(2023广东)某物体由两个相同的正三棱柱组合而成,则其侧面轮廓最不可能是( )。
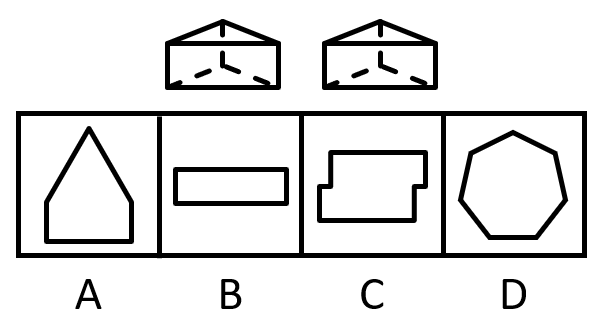
【题型判定】通过题目问题可直接判定本题考查三视图。
【题目分析】本题考查三视图。
本题考查三视图。如下图所示,A、B、C三项按图示摆放,从侧面均可看到图形轮廓,排除;D项无法看到,当选。
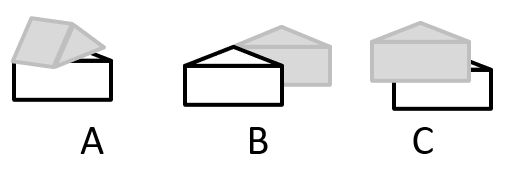
本题为选非题,故正确答案为D。
小粉笔总结
立体拼合、截面图与三视图三种题型的考试内容相对固定,立体拼合题目要遵循“凹凸一致”的解题原则,遇到小方块的拼合题目,当选项小方块数不同时,优先考虑小方块数;截面图除了要掌握截面图与剖面的区别,更要掌握“一刀切”的解题原则,最重要的是常见基础图形的截面形状,即使是难题也可以转换成基础图形再去研究;三视图要了解解题的思路,尤其是立体图形出现遮挡和曲线时,要注意细节的判断。
最后,希望同学们能通过学习,掌握好立体拼合、截面图以及三视图的做题方法和技巧,在备考过程中不断练习,攻克难点,在考场中顺利得分!