
前 言 (方程法)
方程法是解决数学问题最常用的方法之一,在大部分考试中都有题目可以用到方程法。列方程时需注意两点:一是找到等量关系,二是尽量简化计算。方程法的题型有两类:普通方程和不定方程。
一、普通方程
题目中存在明显的等量关系时,可以根据等量关系列出方程。当题干中有“共有…”“多/少…”“刚好相等”“提高/降低了”“比重是”“…倍”等关键词时,即可列方程。一些经典问题中的公式也可作为方程的等量关系,例如
速度×时间=路程,效率×时间=工程量。
方程法具体步骤:
首先设未知数,一般优先设所求量或中间量,然后将其他未知量用未知数表示,最后根据等量关系列方程(组)求解。
例题演示
甲、乙、丙、丁四人共有625元,甲的钱数加上4,等于乙的钱数减去4,等于丙的钱数乘以4,等于丁的钱数除以4。问甲有多少元钱?
A.24
B.96
C.104
D.125
【答案】A
【解析】设甲的钱加上4元后为x元,则根据题意可得:甲有(x-4)元,乙有(x+4)元,丙有x/4元,丁有4x元。
四人共有625元,则可列方程:x-4+x+4+x/4+4x=625,解得x=100,则甲有x-4=100-4=96元。
故正确答案为B。
二、不定方程
当未知数个数多于方程个数,不能通过一般的消元法直接得到唯一解。根据未知数是否为整数,可以将不定方程分为未知数必须是整数(常用来表示人数、物体个数等)、未知数不一定是整数(常用来表示物品的价格等)。
①未知数必须为整数的不定方程解法:首先根据奇偶特性、倍数特性、尾数特性等数字特性法缩小未知数的范围,再结合代入排除法判断。
例题演示
将一批杂志整理进书架,已知每一个大空格可放置54本,每一个小空格能放置36本。现有378本杂志,已知最终每一本杂志都放入书架,每个空格均放满,且小空格不少于7个。则该书架共有大空格( )。
A.1个
B.2个
C.3个
D.4个
【答案】A
【解析】设该书架有小空格个,大空格个。则依题意可得:36x+54y=378,化简得2x+3y=21。根据奇偶性判定,y一定是奇数,排除B、D选项。代入A项:2x+3×1=21,解得x=9>7,符合题意,正确。
故正确答案为A。
②未知数不一定为整数的不定方程解法:赋零法。
例题演示
甲、乙、丙三种货物,若购甲3件、乙7件、丙1件,共需325元;若购甲4件、乙10件、丙1件,共需410元。那么购甲、乙、丙各1件,共需多少元?( )
A.100
B.125
C.135
D.155
【答案】D
【解析】

小粉笔总结
综上,方程是解数量关系题时的常用方法,这一部分内容需要大家做更多相应的题目才能熟练掌握,希望各位考生多多刷题,获得更大的进步。
前 言 ( 数列 )
军队文职考试中注重考查考生的基础能力,计算问题就属于一种,而等差等比数列的应用就属于计算问题当中的一个知识点,因此要求各位考生要掌握一定的数列基础知识,才能在做题的时候得心应手。常考的题型分为两类:等差数列和等比数列,接下来,我们分别来看这两种题型的解题方法。
一、等差数列
等差数列指的是从数列的第二项开始,后一项与前一项的差是固定值。在等差数列中,主要考查等差数列的通项公式与求和公式:
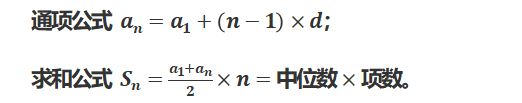
例题演示
一个阶梯教室设有10排座位,前一排比后一排少2个座位,第一排有20个座位,这个阶梯教室共有( )个座位。
A.240
B.280
C.290
D.330
【答案】C
【解析】

二、等比数列
等比数列指的是从第二项起每一项与前一项的比值都是固定值。常用公式也是其通项公式与求和公式。
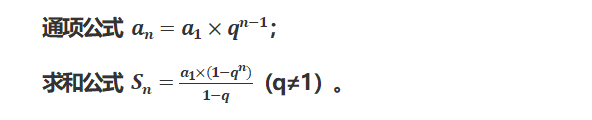
例题演示
某活动设有5个等级奖金,其奖金依次成等比数列关系,已知五等奖的奖金为3000元,三等奖的奖金为3600元。问一等奖的奖金比三等奖要多( )元。
A.650
B.700
C.720
D.750
【答案】C
【解析】

小粉笔总结
需要注意的是,军队文职考试中等比数列问题考查的频率相对来说比较低,重点考查等差数列。
综上,数列问题在考试中考查的频率相对来说比较低,重点考查等差数列。整体来说题目的难度适中,要求考生熟练掌握公式并灵活运用到题目中,注意对题意的整体把握,即可解决数列问题。最后小粉笔祝大家考出好成绩。


