周期问题
周期问题是数学运算中较为重要和高频的一个考点，且难度往往不高，考生往往把握了技巧，基本都会有不错的效果。周期问题往往考查三类题型，分别是周期相遇、周期余数、星期推断，接下来我们分别来看这三种题型。
（一）周期相遇
题型特征：给出多个小周期和首次相遇的时间，求下次相遇的时间。
方法技巧：找到多个小周期的最小公倍数N，过N天（原日期+N天）
注意：每隔a天去1次=每a+1天去1次。
接下来我们通过例题来练习一下：
例题
甲、乙、丙三人去某著名酒吧喝酒，甲每7天去一次，乙每4天去一次，丙每6天去一次，如果2018年6月1日他们在该酒吧相遇，那么下次相遇应该是2018年（ ）。
A.11月15日
B.8月25日
C.8月24日
D.8月23日
【答案】C
【解析】
甲、乙、丙三人下次相遇需要再过各自周期7、4、6的最小公倍数84天。6月1日再过30天是7月1日，再过31天是8月1日，天，8月1日再过23天是8月24日。
故正确答案为C。
（二）周期余数
题型特征：已知某天为周几，求另外某天为周几。
方法技巧：过几天÷7=商…余数，余几星期数加几。
接下来我们通过例题来练习一下：
例题
已知2021年1月1日是星期五，则2021年7月1日是（ ）。
A. 星期一
B. 星期二
C. 星期三
D.星期四
【答案】D
【解析】
2021年1月1日到2021年7月1日过了30+28+31+30+31+30+1=181天，已知一周有7天，则181/7=25……6天，即从星期五过6天，为星期四。
故正确答案为D。
（三）星期推断
题型特征：已知一段时间内有若干个周几，求某天为周几。
方法技巧：连续28天（4周），周一至周日各4天。
接下来我们通过例题来练习一下：
例题
某年的5月有5个星期六、4个星期日，则这年的5月1日是（ ）。
A. 星期一
B.星期二
C.星期三
D.星期四
【答案】D
【解析】
根据常识可知5月份共有31天，每个星期有7天，所以5月份有4个完整的星期余3天。4个星期共有4个星期六和4个星期日，本题已知有5个星期六，所以5月31日对应星期六，5月29日对应星期四，5月1日经过4个星期为5月29日，所以5月1日也为星期四。
故正确答案为D。
数列问题
考试中有些题型注重考查考生的基础能力，计算问题就属于一种，而等差等比数列的应用就属于计算问题当中的一个知识点，因此要求各位考生要掌握一定的数列基础知识，才能在做题的时候得心应手。
常考的题型分为两类：等差数列和等比数列，接下来，我们分别来看这两种题型的解题方法。
（一）等差数列
等差数列指的是从数列的第二项开始，后一项与前一项的差是固定值。在等差数列中，主要考查等差数列的通项公式与求和公式：
1.通项公式：
=a₁+（n-1）×d；
2.求和公式：
=中位数×项数
例题
有一堆粗细均匀的圆木，最上面一层有6根，每向下一层增长一根，共堆了25层。这堆圆木共有（ ）根。
A.175
B.200
C.375
D.450
【答案】D
【解析】
由题意可知，最下面一层圆木数量为30根，各层圆木的数量构成首项为6、末项为30、项数为25、公差为1的等差数列。根据等差数列求和公式：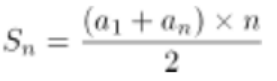
，可得这堆圆木共有(6+30)×25/2=450根。
故正确答案为D。
（二）等比数列
等比数列指的是从第二项起每一项与前一项的比值都是固定值。常用公式也是其通项公式与求和公式。
1. 通项公式：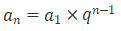
2. 求和公式：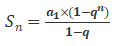
（q≠1）
例题
小蚂蚱向草丛跳，第一跳0.8米，以后每跳比前一次缩短20%，8次后力竭，那么8跳总路程最接近的是（ ）米。
A.3.5
B.4
C.4.5
D.5
【答案】A
【解析】
由题意可知，8次跳跃的路程可构成首项为0.8，公比为1-20%=80%即0.8的等比数列，则8跳总路程为等比数列前8项之和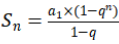
=0.8×(1-0.8⁸)/(1-0.8)=4×(1-0.8⁸)≈4×(1-0.16)=3.36米，与A项最接近。
故正确答案为A。
