
最值问题
最不利构造类
(一)题型特征
问法中出现“至少……保证……”或类似表述。
(二)解题思路
①找出最不利情况,即在题目所要“保证……”的要求不被实现的情况下,尽可能地取到最多;
②答案=最不利情况+1。
构造数列类
(一)题型特征
题目中的总量一定,问法为“最多/少的……至多/少……”“排名第N的至多/少……”。
(二)解题思路
①排序定位:根据主体大小依次排序;
②反向构造:要使某个值尽可能大,则其他的数应尽可能小;反之,要使某个值尽可能小,则其他的数应尽可能大;
③加和求解:总数一定,全部加和求解答案。
(三)注意事项
最后计算出来的结果是非整数时,不能四舍五入,需要结合题干的问法进行判断。若问最少,计算后应该向上取整;若问最多,计算后应该向下取整。比如:最后计算结果是7.5,若问最少,则结果应该选8;若问最多,则结果应该选7,这就是向上、向下取整的意思。
最值思维类
(一)题型特征
根据题干可列出不定方程(组),和为定值,问其中一部分最多/最少是多少。
(二)解题思路
①此消彼长;
②找极端情况。
溶液问题
溶液混合类
(一)题型特征
溶液混合问题一般难度不大,且命题有一定套路性,常考的有两溶液混合与三溶液混合。
(二)解题思路
①两种溶液混合时,若已知混合前两种溶液的浓度,用线段法(混合之前写两边,混合之后写中间;距离(浓度差)与量(溶液的重量)成反比,看好份数认真算);
②两种溶液混合时,若不知混合前两种溶液的浓度,用公式法(浓度=溶质/溶液);
③三种溶液混合时,建议用公式法。
溶质不变类
(一)题型特征
当浓度问题中出现某种溶液蒸发掉一部分水,或出现在溶液中加水,但溶质的质量不变,此时即为溶质不变类浓度问题。
(二)解题思路
①没有出现具体数值,设溶质为一个不变量;
②利用溶质不变建立等量关系,原来的溶质=现在的溶质。
溶液不变类
(一)题型特征
当浓度问题中出现将某种浓度的溶液倒出一部分后再加满水,来回反复保持溶液总量不变,或出现将两种浓度不同的溶液相互倒出若干次,但每种溶液总量保持不变,此时即为溶液不变类浓度问题。
(二)解题思路
①浓度为r的溶液,倒出a%,再加满水,浓度会变成r×(1-a%);
②溶液不变,只分析溶质变化即可。
计数问题
方阵问题
(一)题型特征
若干个主体排列成方阵,求主体的个数。
(二)解题思路
①正方形方阵边长为n,则最外层人数=4n-4;长方形方阵长边为a,短边为b,则最外层人数=2(a+b)-4;
②正方形方阵边长为n,则实心正方形方阵的总人数=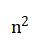 ;长方形方阵长边为a,短边为b,则实心长方形方阵的总人数=a×b;
;长方形方阵长边为a,短边为b,则实心长方形方阵的总人数=a×b;
③相邻两层人数相差为8。此结论在空心方阵计算总人数时会用到。
方阵问题套路性强,掌握方法即可解题。计算总人数时,可理解为求四边形的面积,正方形为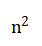 ,长方形为a×b。另外,解题时若没有明确说是空心方阵,则一般默认为实心方阵。
,长方形为a×b。另外,解题时若没有明确说是空心方阵,则一般默认为实心方阵。
植树问题
(一)题型特征
在道路两边植树或摆放物品、安装路灯等,求种植棵数(摆放个数、安装个数)。
(二)解题思路
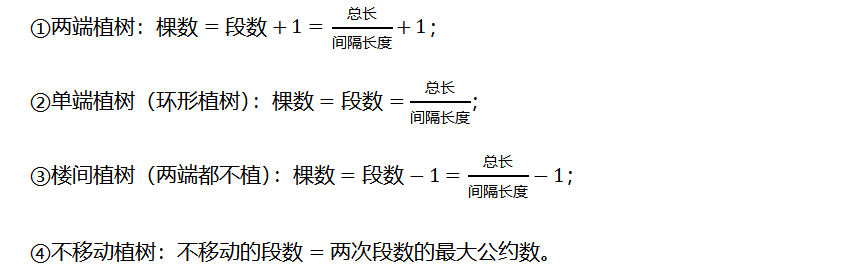
求不移动棵数时,若是两端植树,则=最大公约数+1;若是单端植树,则=最大公约数;若是楼间植树,则=最大公约数-1。
